32. The Identity Matrix
The Identity Matrix
The identity matrix is a special matrix in linear algebra that shows up in quite a few applications. For the purposes of this lesson, gaining insight into the identity matrix will help you understand matrix inversion. The identity matrix is represented by the symbol \mathbf{I}.
\mathbf{I} is an n x n square matrix with 1 across the main diagonal and 0 for all other elements.
For a 1x1 matrix, the identity matrix looks like this:
\begin{bmatrix}1\end{bmatrix}
A 2x2 identity matrix looks like this:
\begin{bmatrix}1 & 0 \\ 0 & 1\end{bmatrix}
The 3x3 identity matrix is the following:
\begin{bmatrix}1 & 0 & 0 \\0 & 1 & 0 \\0 & 0 & 1\end{bmatrix}
The 4x4 identity matrix is:
\begin{bmatrix}1 & 0 & 0 & 0 \\0 & 1 & 0 & 0 \\0 & 0 & 1 & 0 \\0 & 0 & 0 & 1\end{bmatrix}
and so on.
Identity Matrix is like the Number One
In scalar multiplication, the number one has a special property:
1\times a = a.
Likewise,
a\times 1 = a.
It turns out the Identity matrix has the same property:
\mathbf{AI} = \mathbf{IA} = \mathbf{A}. And although the identity matrix is always square, matrix \mathbf{A} does not have to be square.
Here is an example of multiplying
\mathbf{AI}
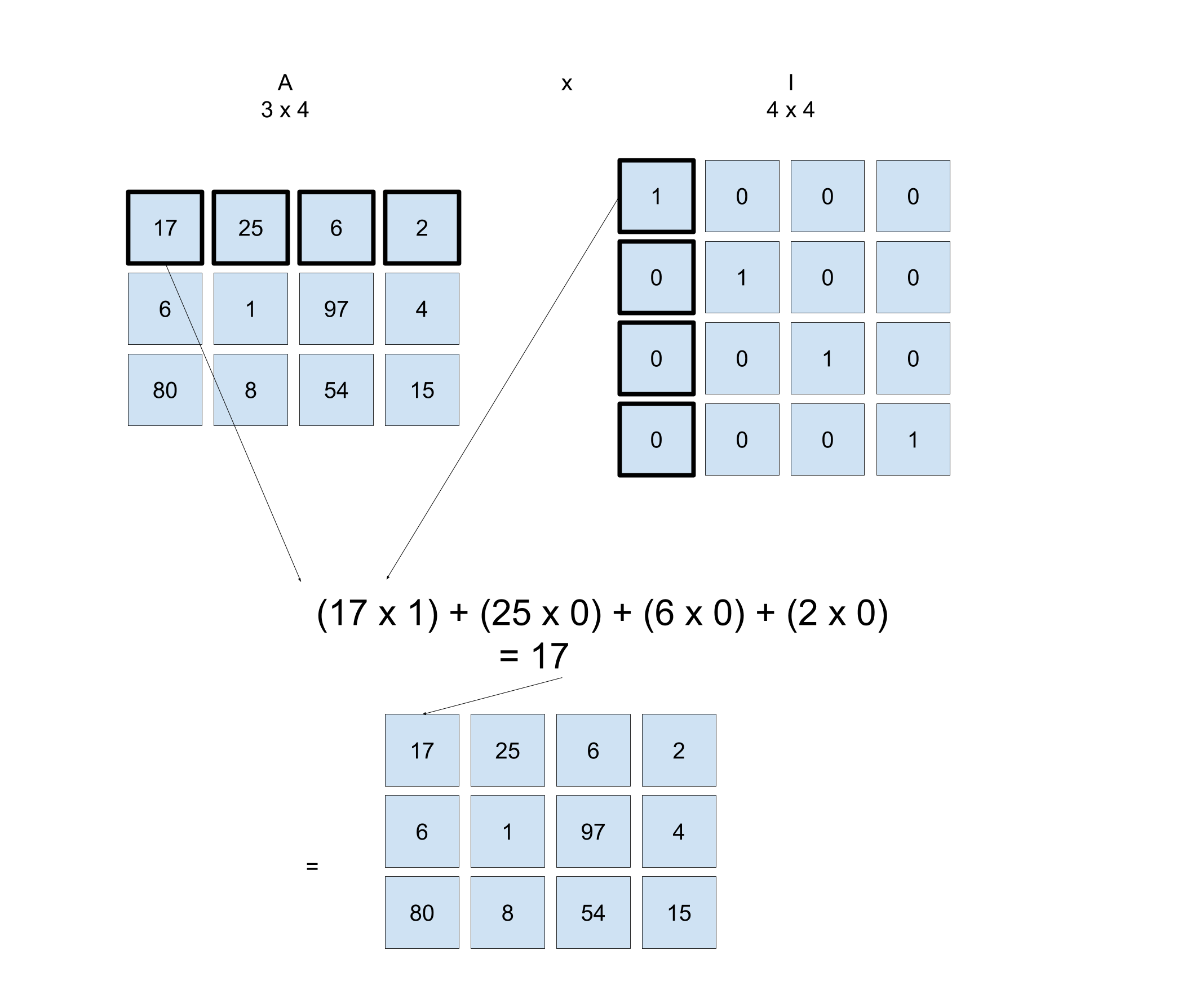
What about the other case of multiplying \mathbf{IA}? You'll need to take into account the dimensions of the I and A matrix so that the multiplication works.
How do you figure out the size of \mathbf{I}?
The output matrix has to be 3x4 just like \mathbf{A}. So a 3x3 matrix multiplied by a 3x4 matrix will give a 3x4 matrix.
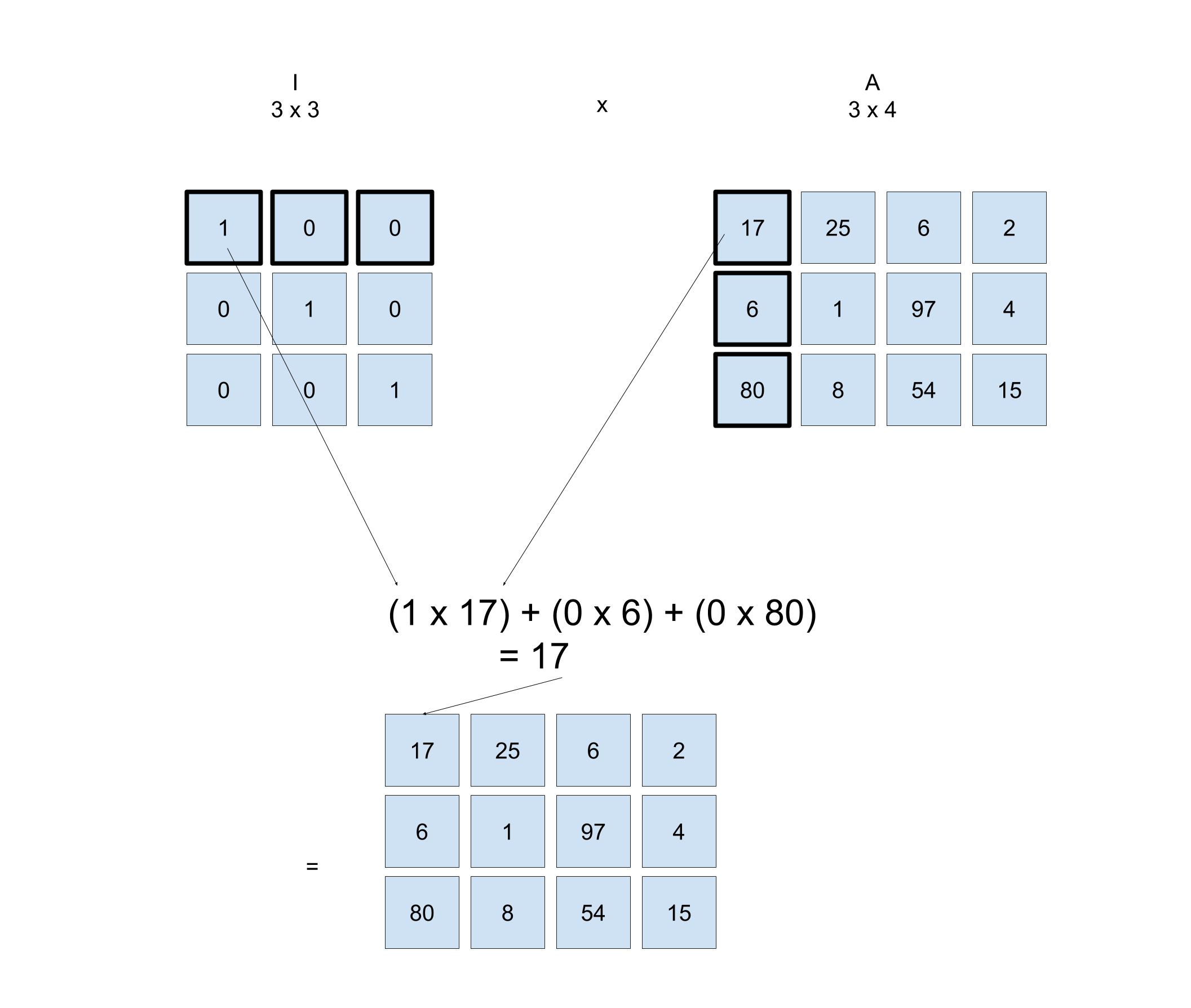
Size of I
SOLUTION:
5x5 and 7x7Initializing an Identity Matrix with Code
In the coding exercise, you will write a function that receives a size and outputs the identity matrix for that size.
Think about how you might go about coding this starting from an empty Python list. The ones will always be at indicies
- [0][0]
- [1][1]
- [2][2]
- [3][3]
- etc.
Everywhere else in the matrix will be zero. So you will need to not only use nested for loops but also if else statements.